(GLUT)球の衝突のアニメーション

アニメ『ダーリン・イン・ザ・フランキス』(2018)

コドモたちが戦うロボットアニメ。ドキっとするシーン多いです。何も知らない無垢なコドモたちだから余計に。劇中、他都市とのキッシングって言葉が出てきたのですが、キッシングでWeb検索すると魚釣りのことばかりでてきます。もちろん魚とは無関係ですね。ビリヤードの球のキス（衝突）のイメージでしょうか。タイトルの×マークも含めて言葉の使い方がかっこいいです。

さて球の衝突を考えてみます。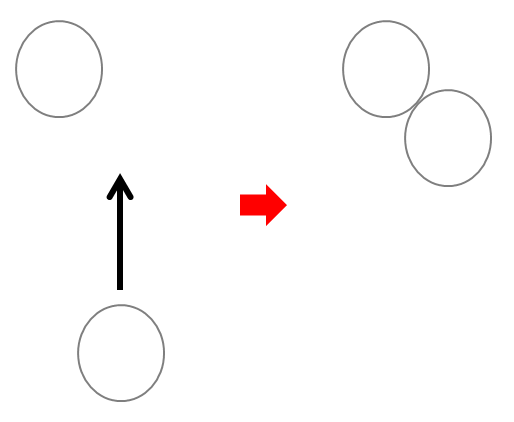

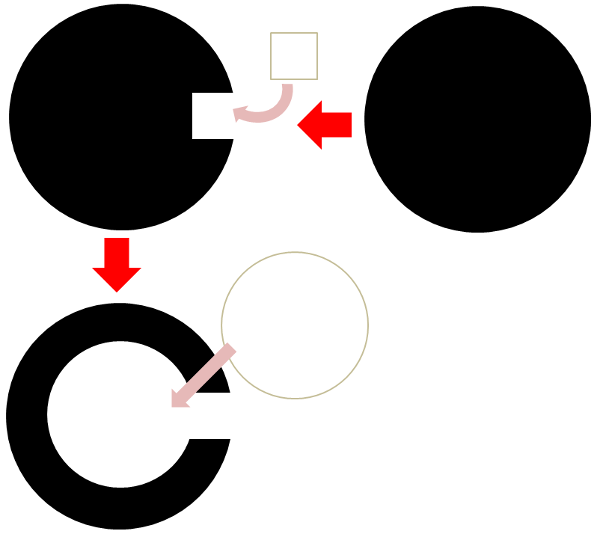
今回作るのは、図のように同じ大きさの球を、片方だけ移動させて、もう片方と衝突した時に停止するアニメーションのプログラムです。

球なので、球A、球Bの接点は、球Aの中心から、球Bの中心までの距離が、半径の二倍の距離に一致します。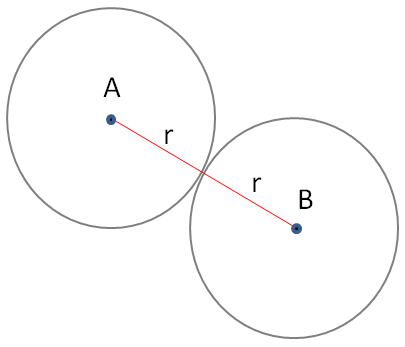

衝突時の各球の座標を求めるには、ピタゴラスの定理で求めることができます。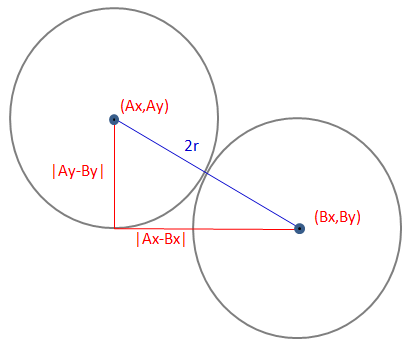

つまり二つの球が衝突するのは、この条件の位置関係の時となります。
$$\LARGE{2r=\sqrt{(Ax-Bx)^2 + (Ay-By)^2}}$$
プログラムです。

takk@deb9:~$ cat -n collision1.c
     1  #include <GL/glut.h>
     2  #include <math.h>
     3
     4  #define DEG2RAD(deg) deg * 2.0 * M_PI / 360.0
     5  #define WHITE 1.0, 1.0, 1.0, 0.0
     6  #define BLACK 0.0, 0.0, 0.0, 0.0
     7
     8  GLdouble Ax,Ay;
     9  GLdouble Bx,By;
    10

グローバル変数で各球の位置を定義。

    11  void polygon(GLdouble x, GLdouble y, int n, GLdouble r)
    12  {
    13          int i;
    14          double deg;
    15
    16          glBegin(GL_LINE_LOOP);
    17          glColor4f(BLACK);
    18
    19          for(i=0; i<n; i++){
    20                  deg = (360.0/n) * i;
    21                  glVertex2d(
    22                          x + r * cos(DEG2RAD(deg)),
    23                          y + r * sin(DEG2RAD(deg)));
    24          }
    25          glEnd();
    26  }
    27
    28  void callback_display()
    29  {
    30          glClearColor(WHITE);
    31          glClear(GL_COLOR_BUFFER_BIT);
    32
    33          polygon(Ax, Ay, 30, 0.1);
    34          polygon(Bx, By, 30, 0.1);
    35
    36          glFlush();
    37  }
    38

33,34行目で球(円)を描きます。実際は、30角形です。半径は0.1を指定。

    39  void callback_timer(int value)
    40  {
    41          double c;
    42          c = sqrt(pow(Ax-Bx, 2) + pow(Ay-By, 2));
    43          if((int)(c*1000) != 200)
    44                  By += 0.001;
    45          glutPostRedisplay();
    46          glutTimerFunc(1,callback_timer,0);
    47  }
    48

44行目で、球Bを上に0.001ずつ移動させますが、42行目の衝突位置の計算で、衝突したと判断した場合は、球Bの移動をやめます。
球の半径が0.1ですので、各球の中心と中心との距離が0.2になれば衝突と判定します。1000倍してint型でキャストして判定。

    49  int main(int argc, char *argv[])
    50  {
    51          Ax=0.0;Ay= 0.4;
    52          Bx=0.1;By=-0.8;
    53          glutInit(&argc, argv);
    54          glutInitDisplayMode(GLUT_RGBA);
    55          glutCreateWindow("COLLISION1");
    56
    57          glutTimerFunc(1,callback_timer,0);
    58          glutDisplayFunc(callback_display);
    59
    60          glutMainLoop();
    61
    62          return 0;
    63  }
takk@deb9:~$

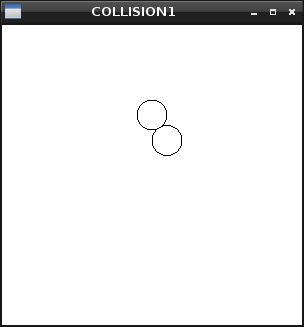
プログラムを実行すると、下の球が上方向に移動し、上の球と接した時、停止するアニメーションが見れます。

takk@deb9:~$ gcc -lglut -lGLU -lGL -lm collision1.c
takk@deb9:~$ ./a.out