https://www.youtube.com/watch?v=b2QM_0vNpzE
アニメ『キン肉マン』
前回ラーメンマンを描いて、キン肉マンを思い出したので、アニメ1話目も見てみました。
なんとキン肉マンが巨大化。昔見た記憶ではプロレスバトルのことしか覚えてなかったので、簡単に巨人になれることに衝撃を受けました。1話目からテリーマン出てきますが、最初はいけ好かないキャラだったんですね。この二人がいずれ熱い友情でタッグを組むんですね。
では夢の超人タッグ編でブラックホールを引き連れて急にカッコよく登場するペンタゴンの五芒星を描いてみます。
まずは「(GLUT)三角形を描く」で作った三角形を描くプログラムを、多角形にも対応するように改造します。
1 #include <GL/glut.h>
2 #include <math.h>
3
4 #define DEG2RAD(deg) deg * 2.0 * M_PI / 360.0
5 #define WHITE 1.0, 1.0, 1.0, 0.0
6 #define RED 1.0, 0.0, 0.0, 0.0
7
8 void polygon(GLdouble x, GLdouble y, int n, GLdouble r)
9 {
10 GLdouble xx, yy;
11 int i;
12 double deg,offs = 90.0;
13
14 glBegin(GL_LINE_LOOP);
15 glColor4f(RED);
16
17 for(i=0; i<n; i++){
18 deg = (360.0/n) * i + offs;
19 xx = x + r * cos(DEG2RAD(deg));
20 yy = y + r * sin(DEG2RAD(deg));
21 glVertex2d(xx, yy);
22 }
23
24 glEnd();
25 }
26
27 void callback_display()
28 {
29 glClearColor(WHITE);
30 glClear(GL_COLOR_BUFFER_BIT);
31
32 polygon(0, 0, 3, 0.5);
33
34 glFlush();
35 }
36
37 int main(int argc, char *argv[])
38 {
39 glutInit(&argc, argv);
40 glutInitDisplayMode(GLUT_RGBA);
41 glutCreateWindow("Polygon1");
42
43 glutDisplayFunc(callback_display);
44
45 glutMainLoop();
46
47 return 0;
48 }
49
多角形は英語でpolygonなので、polygonという関数名で、引数でxy座標と頂点数とサイズを指定できるように処理を関数化しました。
polygon(x, y, 頂点数, 中心からのサイズ)
三角形が描画できるか、3を指定して実行してみます。
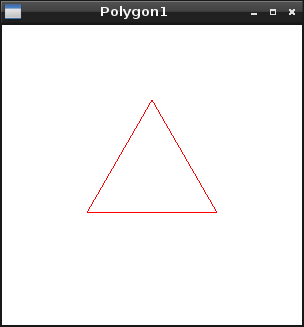
次は、4~12までの数を指定して実行。
1 void callback_display()
2 {
3 glClearColor(WHITE);
4 glClear(GL_COLOR_BUFFER_BIT);
5
6 polygon(-0.5, 0.5, 4, 0.2);
7 polygon(-0.5, 0.0, 5, 0.2);
8 polygon(-0.5,-0.5, 6, 0.2);
9
10 polygon( 0.0, 0.5, 7, 0.2);
11 polygon( 0.0, 0.0, 8, 0.2);
12 polygon( 0.0,-0.5, 9, 0.2);
13
14 polygon( 0.5, 0.5,10, 0.2);
15 polygon( 0.5, 0.0,11, 0.2);
16 polygon( 0.5,-0.5,12, 0.2);
17
18 glFlush();
19 }

では、ペンタゴンの五芒星を描きましょう。頂点数は5で良いのですが、これではただの五角形になってしまうので少し改造します。
元の関数のdeg=の行を、
void polygon(GLdouble x, GLdouble y, int n, GLdouble r)
{
~省略~
for(i=0; i<n; i++){
deg = (360.0/n) * i + offs;
~省略~
i*2にして、一つ飛ばしにするだけです。
for(i=0; i<n; i++){
deg = (360.0/n) * i*2 + offs;
呼び出し時の頂点数は5を指定。
void callback_display()
{
~省略~
polygon(0, 0, 5, 0.5);
~省略~
できました。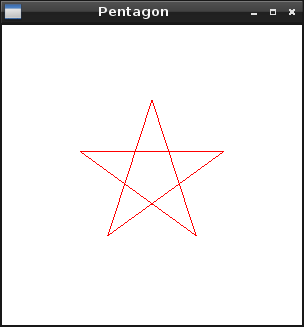


コメント